Computing optimal capital and labor

This function computes the optimal choice of capital and labor for all combinations of state of assets and productivity based on degree of imperfect enforcement of contracts

Back to full code page https://kritikhanna.github.io/BKS-modified/

Function Inputs : asset grid(1 by M) and entrepreneurial productivity grid(1 by N) relevant model parameters required to compute the constraint on capital and labor based on the degree of contract enforceability.

Function Outputs : Matrices k star and l star (both M X N) for each combination of a and z. mt_id returns index of min of contstraint k and unconstrained k

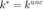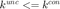
$k^{*} = k^{unc}$ , if $k^{unc} <= {k}^{con}$

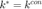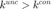
$k^{*} = {k}^{con}$ , if $k^{unc} > {k}^{con}$

Set Parameters
Set Controls
Mesh Grids
Optimal Unconstrained
Optimal Constrained
3D Plots for k* and l*
2D plot for k*

function [mt_k_star, mt_l_star, mt_id]=optikl(varargin)

close all;
bl_profile = false;      % Switch off profile if running a tester/calling from another function
bl_saveimg = false;
if(bl_profile)
profile off;
profile on;
end

addpath(genpath('/Users/sidhantkhanna/Documents/GitHub/BKS modified/'));


if ~isempty(varargin)

    [ar_a,ar_z, ...
        fl_alpha,fl_theta,fl_delta,fl_kappa,fl_r,fl_w,fl_phi,fl_ahi,fl_zhi, ...
         it_zgridno, it_agridno, ...
        ] = varargin{:};

    bl_print  = false;
    bl_plot   = false;

else
    close all;

    fl_ahi         = 5;
    fl_zhi         = 2.2;
    it_agridno     = 5;
    it_zgridno     = 6;
    ar_a = linspace(0,fl_ahi,it_agridno);
    ar_z = linspace(1,fl_zhi,it_zgridno);
    fl_phi         = 0.1;

    fl_alpha = 0.4;
    fl_theta = 0.79-fl_alpha;
    fl_delta = 0.05;
    fl_kappa = 0;

    [fl_r,fl_w,fl_ahi] = ...
        deal(0.05,3,100);
    bl_print       = true;
    bl_plot        = true;

end

Set Parameters

fl_R = fl_r + fl_delta;

Set Controls

bl_constrained = true;
if( fl_phi == 1)
    bl_constrained = false;
end
bl_feas = true; %

Mesh Grids

[a_m,z_m] = meshgrid(ar_a,ar_z);    % creates 2 matrices of size it_zgridno x it_agridno
                                    % a_m has it_zgridno no. of identical rows, each row is ar_a. So each column
                                    % has identical a element repeated it_zgridno times
                                    % z_m has it_agridno no of identical columns, each column is ar_z. So each
                                    % row has identical z element repeated it_agridno times

ar_a_v = a_m(:);                    % matrix unlayered one column under another
ar_z_v = z_m(:);                    % matrix unlayered one column under another


ar_k_unc = exp((log(fl_R./(ar_z_v.*fl_alpha))- fl_theta*log(fl_R./(ar_z_v.*fl_alpha))+ fl_theta.*log(fl_w./(ar_z_v.*fl_theta)))./(fl_alpha+fl_theta-1));
ar_l_unc = exp((log(fl_w./(ar_z_v.*fl_theta))+ fl_alpha*log(fl_R./(ar_z_v.*fl_alpha))- fl_alpha.*log(fl_w./(ar_z_v.*fl_theta)))./(fl_alpha+fl_theta-1));

mt_k_unc = reshape(ar_k_unc, [it_zgridno,it_agridno]);
mt_l_unc = reshape(ar_l_unc, [it_zgridno,it_agridno]);

mt_k_unc = mt_k_unc';
mt_l_unc = mt_l_unc';

Optimal Unconstrained

if (~bl_constrained)

    % in the constrained case, a can not matter, but z does matter
    if(bl_feas)
    feas  = (1+fl_r)*fl_kappa;
    feas_v = ar_z_v.*ar_k_unc.^fl_alpha.*ar_l_unc.^fl_theta;
    for i = 1:numel(ar_a_v)
       if (feas_v(i)<feas)
       ar_k_unc(i) = 0;
       ar_l_unc(i) = 0;
       end
    end
    end

    mt_k_unc = reshape(ar_k_unc, [it_zgridno,it_agridno]);
    mt_l_unc = reshape(ar_l_unc, [it_zgridno,it_agridno]);

    mt_k_unc = mt_k_unc';
    mt_l_unc = mt_l_unc';

    mt_k_star = mt_k_unc;
    mt_l_star = mt_l_unc;
    mt_id     = ones(it_zgridno,it_agridno);    % index of min between constraint k and unconstraned k


if( bl_print)
    disp('Below is mt_k_star')
    disp(size(mt_k_star));
    disp(mt_k_star);
    disp('Below is mt_l_star')
    disp(size(mt_l_star));
    disp(mt_l_star);
end

else

Optimal Constrained

    % calls function con_kl to evaluate the constraint on capital
    [ar_k_bar,ar_l_bar] = con_kl(ar_a_v, ar_z_v,ar_a,ar_z, fl_ahi,fl_zhi,fl_phi,fl_theta,fl_alpha,fl_w,fl_r,fl_delta,fl_kappa,it_agridno,it_zgridno);

    mt_k_bar=reshape(ar_k_bar, [it_zgridno,it_agridno]);
    mt_l_bar=reshape(ar_l_bar, [it_zgridno,it_agridno]);

    mt_k_bar = mt_k_bar';
    mt_l_bar = mt_l_bar';


    k3        = [ar_k_unc,ar_k_bar];
    [k4,id]   = min(abs(k3'));            % K star is min of k_unc and k_con. k3 transposed for the correct order for id
    ar_k_star = k4';
    l3        =[ar_l_unc,ar_l_bar];
    ar_l_star = zeros(numel(ar_a_v),1);    % assigning l star in constrained case

    for i = 1:numel(ar_a_v)
        ar_l_star(i,1)=l3(i,id(i));
    end

    if(bl_feas)
    feas  = (1+fl_r)*fl_kappa;
    feas_v = ar_z_v.*ar_k_star.^fl_alpha.*ar_l_star.^fl_theta;
    for i = 1:numel(ar_a_v)
       if (feas_v(i)<feas)
       ar_k_star(i) = 0;
       ar_l_star(i) = 0;
       end
    end
    end


mt_k_star=reshape(ar_k_star, [it_zgridno,it_agridno]);
mt_l_star=reshape(ar_l_star, [it_zgridno,it_agridno]);
mt_id = reshape(id, [it_zgridno,it_agridno]);

 mt_k_star=mt_k_star';
 mt_l_star=mt_l_star';
 mt_id = mt_id';

if( bl_print)
    disp('Below is mt_k_unc')
    disp(size(mt_k_unc));
    disp(mt_k_unc);
    disp('Below is mt_k_con')
    disp(mt_k_bar);
    disp('Below is mt_k_star')
    disp(size(mt_k_star));
    disp(mt_k_star);
    disp('Below is mt_l_unc')
    disp(size(mt_l_unc));
    disp(mt_l_unc);
    disp('Below is mt_l_con')
    disp(mt_l_bar);
    disp('Below is mt_l_star')
    disp(mt_l_star);


end

if(bl_plot)

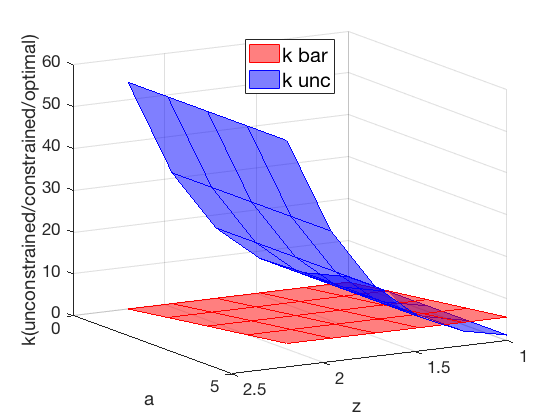
3D Plots for k* and l*

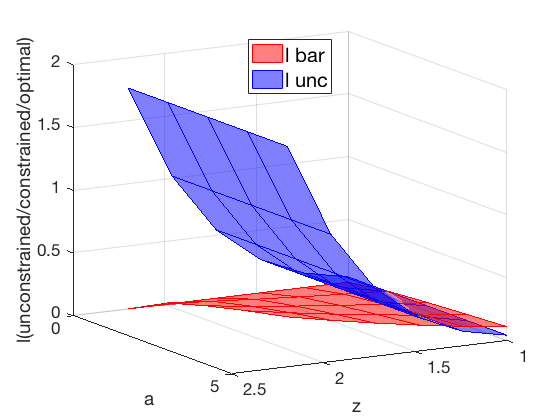
figure (1)
a1 = surf(ar_z, ar_a, mt_k_bar , 'FaceColor','r', 'FaceAlpha',0.5, 'EdgeColor','r'); M1 = 'k bar';
hold on
a2 = surf(ar_z, ar_a, mt_k_unc , 'FaceColor','b', 'FaceAlpha',0.5, 'EdgeColor','b'); M2 = 'k unc';
%hold on
%a3 = surf(ar_z, ar_a, mt_k_star,'FaceColor','g', 'FaceAlpha',0.5, 'EdgeColor','g'); M3 = 'k star' ;
hold off
xlabel('z');
ylabel('a');
zlabel('k(unconstrained/constrained/optimal)');
LEG = legend([a1;a2], M1, M2, 'Location','north')
LEG.FontSize = 20;
view(150,15);
set(gca,'FontSize',17)
if(bl_saveimg)
saveas(gcf, '/Users/sidhantkhanna/Documents/GitHub/BKS modified/code/Firms/figures/optikl/Optimum_k.png')
end

figure (2)
b1 = surf(ar_z, ar_a, mt_l_bar, 'FaceColor','r', 'FaceAlpha',0.5, 'EdgeColor','r'); N1 = 'l bar';
hold on
b2 = surf(ar_z, ar_a, mt_l_unc, 'FaceColor','b', 'FaceAlpha',0.5, 'EdgeColor','b'); N2 = 'l unc';
%hold on
%b3 = surf(ar_z, ar_a, mt_l_star,'FaceColor','g', 'FaceAlpha',0.5, 'EdgeColor','g'); N3 = 'l star' ;
hold off
xlabel('z');
ylabel('a');
zlabel('l(unconstrained/constrained/optimal)');
LEG = legend([b1;b2], N1, N2, 'Location','north')
LEG.FontSize = 20;
view(150,15);
set(gca,'FontSize',17)
if(bl_saveimg)
saveas(gcf, '/Users/sidhantkhanna/Documents/GitHub/BKS modified/code/Firms/figures/optikl/Optimum_l.png')
end

LEG = 

  Legend (k bar, k unc) with properties:

         String: {'k bar'  'k unc'}
       Location: 'north'
    Orientation: 'vertical'
       FontSize: 9
       Position: [0.4604 0.8429 0.1143 0.0631]
          Units: 'normalized'

  Use GET to show all properties


LEG = 

  Legend (l bar, l unc) with properties:

         String: {'l bar'  'l unc'}
       Location: 'north'
    Orientation: 'vertical'
       FontSize: 9
       Position: [0.4630 0.8429 0.1089 0.0631]
          Units: 'normalized'

  Use GET to show all properties

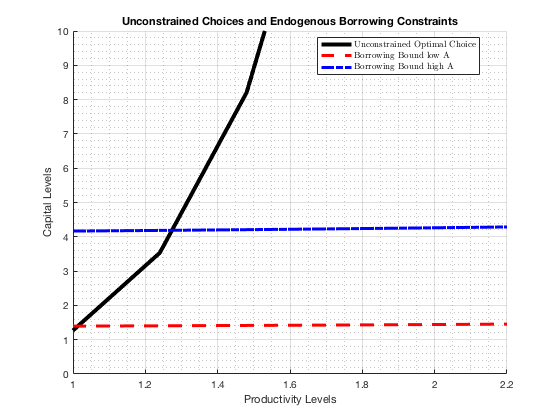
2D plot for k*

% Jet color Graph All
figure(3);
hold on;

% one line, unconstrained choice
pl_unc = plot(ar_z, mt_k_unc(1,:));
pl_unc.HandleVisibility = 'on';
pl_unc.LineStyle = '-';
pl_unc.Color = 'black';
pl_unc.LineWidth = 4;

% one constrained choice line, low a
pl_unc = plot(ar_z, mt_k_bar(2,:));
pl_unc.HandleVisibility = 'on';
pl_unc.LineStyle = '--';
pl_unc.Color = 'red';
pl_unc.LineWidth = 3;

% one constrained choice line, high a
pl_unc = plot(ar_z, mt_k_bar(4,:));
pl_unc.HandleVisibility = 'on';
pl_unc.LineStyle = '-.';
pl_unc.Color = 'blue';
pl_unc.LineWidth = 3;

% additional options
grid on;
grid minor;
xlim([1, 2.2]);
ylim([0, 10]);

title('Unconstrained Choices and Endogenous Borrowing Constraints');
ylabel('Capital Levels');
xlabel({'Productivity Levels'});
legend({'Unconstrained Optimal Choice',...
        'Borrowing Bound low A', ...
        'Borrowing Bound high A'}, 'Location', 'best', 'Interpreter','latex');

if(bl_saveimg)
saveas(gcf, '/Users/sidhantkhanna/Documents/GitHub/BKS modified/code/Firms/figures/optikl/Optimum_2D.png')
end

hold off;

end

Below is mt_k_unc
     5     6

    1.2685    3.5332    8.2050   16.7831   31.2610   54.1865
    1.2685    3.5332    8.2050   16.7831   31.2610   54.1865
    1.2685    3.5332    8.2050   16.7831   31.2610   54.1865
    1.2685    3.5332    8.2050   16.7831   31.2610   54.1865
    1.2685    3.5332    8.2050   16.7831   31.2610   54.1865

Below is mt_k_con
    0.0000    0.0000    0.0000    0.0001    0.0002    0.0003
    1.3959    1.4052    1.4157    1.4276    1.4407    1.4551
    2.7826    2.7971    2.8136    2.8321    2.8526    2.8748
    4.1672    4.1861    4.2076    4.2316    4.2581    4.2870
    5.5507    5.5735    5.5994    5.6283    5.6602    5.6949

Below is mt_k_star
     5     6

    0.0000    0.0000    0.0000    0.0001    0.0002    0.0003
    1.2685    1.4052    1.4157    1.4276    1.4407    1.4551
    1.2685    2.7971    2.8136    2.8321    2.8526    2.8748
    1.2685    3.5332    4.2076    4.2316    4.2581    4.2870
    1.2685    3.5332    5.5994    5.6283    5.6602    5.6949

Below is mt_l_unc
     5     6

    0.0412    0.1148    0.2667    0.5454    1.0160    1.7611
    0.0412    0.1148    0.2667    0.5454    1.0160    1.7611
    0.0412    0.1148    0.2667    0.5454    1.0160    1.7611
    0.0412    0.1148    0.2667    0.5454    1.0160    1.7611
    0.0412    0.1148    0.2667    0.5454    1.0160    1.7611

Below is mt_l_con
    0.0000    0.0000    0.0001    0.0002    0.0004    0.0007
    0.0439    0.0627    0.0843    0.1084    0.1351    0.1643
    0.0690    0.0985    0.1322    0.1698    0.2114    0.2568
    0.0899    0.1283    0.1721    0.2210    0.2749    0.3337
    0.1085    0.1548    0.2076    0.2664    0.3313    0.4020

Below is mt_l_star
    0.0000    0.0000    0.0001    0.0002    0.0004    0.0007
    0.0412    0.0627    0.0843    0.1084    0.1351    0.1643
    0.0412    0.0985    0.1322    0.1698    0.2114    0.2568
    0.0412    0.1148    0.1721    0.2210    0.2749    0.3337
    0.0412    0.1148    0.2076    0.2664    0.3313    0.4020

end

if(bl_profile)
profile off;
profile viewer;
st_file_name = '/Users/sidhantkhanna/Documents/GitHub/BKS modified/code/Profile/Firms/optikl';
profsave(profile('info'), st_file_name);


end