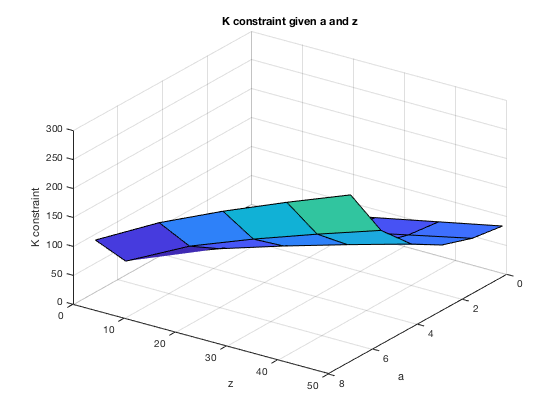
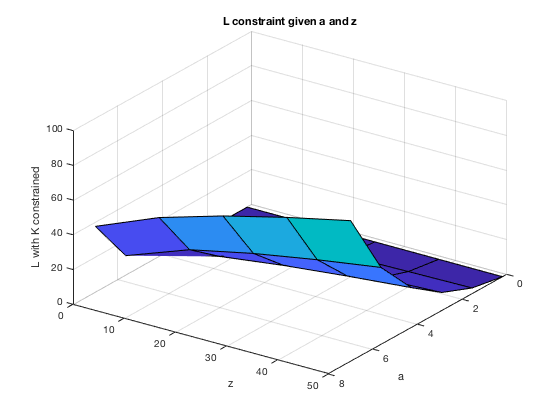
Computing constraint on capital and corresponding optimal labor
This function computes the constraint on borrowing of capital and corresponding optimal labor for all combinations of state of assets and productivity based on degree of imperfect enforcement of contracts. Uses 3 methods- Numerical, Vectorized, Taylor Series
Back to full code page https://kritikhanna.github.io/BKS-modified/
Function Inputs : Meshed-vectorised asset grid (size = it_agridnoxit_zgridno x 1) and entrepreneurial productivity grid (size : it_agridnoxit_zgridnox1), relevant model parameters required to compute the constraint on capital and labor based on the degree of contract enforceability.
Function Outputs : Returns an array of k and l (meshed-vectorized, size = it_agridnoxit_zgridno x 1 ), which are constrained k and l for each combination of assets and and entrepreneurial productivity. Also generates and prints matrix of constrained k and l.
Contents
function [ar_k_con,ar_l_con]=con_kl(varargin)
close all; bl_profile = false; % Switch off profile if running a tester/calling from another function if(bl_profile) profile off; profile on; end addpath(genpath('/Users/sidhantkhanna/Documents/GitHub/BKS modified/')); if ~isempty(varargin) [ar_a_v,ar_z_v,ar_a,ar_z ... fl_ahi,fl_zhi, fl_phi,fl_theta,fl_alpha,fl_w,fl_r,fl_delta,... fl_kappa,it_agridno,it_zgridno, ... ] = varargin{:}; % Display matrix and graphs of constrained k and l (for every combination of a and z) % if testing the index below, print out graph, and also show each % iteration of the first order taylor approximation. if bl_state_test % is true, then test specific state iteration to arrive at \bar{k}. bl_print = false; bl_state_test = false; it_test_a_idx = 1; it_test_z_idx = 1; bl_saveimg = false; % True if images are to be saved, false if you want to publish them it_k_n = 20000; % capital grid points to create capital grid and search for else
fl_ahi = 50;
fl_zhi = 7;
it_agridno = 5;
it_zgridno = 6;
ar_a = linspace(0,fl_ahi,it_agridno); % Sample asset grid
ar_z = linspace(0.2,fl_zhi,it_zgridno); % Sample entrepreneurial productivity grid
%ar_a = 50; % for testing single a value
%ar_z = 1; % for testing single z value
[a_m,z_m] = meshgrid(ar_a,ar_z); % Meshed matrix of assets and entrepreneurial productivity
% grid (size for a_m = it_zgridnoxit_agridno, z_m =it_zgridnoxit_agridno)
ar_a_v = a_m(:); % Meshed-vectorised asset grid
ar_z_v = z_m(:); % Meshed-vectorised entrepreneurial productivity grid
it_k_n = 20000; % capital grid points to create capital grid and search for
% constrained k
fl_phi = 0.5;
fl_alpha = 0.4;
fl_theta = 0.79 - fl_alpha;
fl_delta = 0.06;
fl_kappa = 2;
[fl_r,fl_w,fl_ahi] = ...
deal(0.04,1.8,100);
Testing Controls
bl_print = true; % Print matrix of optimal k with graphs bl_state_test = true; % Plotting taylor method graphs for root finding it_test_a_idx = 2; % a index for drawing graph or root search of k using TS approx it_test_z_idx = 4; % z index for drawing graph or root search of k using TS approx bl_saveimg = false;
end
Parameter controls
it_max_iter_taylor = 7; % No of iterations for taylor series approximation for constraint function
Initialize Matrices
fl_R = fl_r + fl_delta; mt_k_con = ones(it_agridno,it_zgridno); % Matrix for storing constrained k , for each combination on a and z mt_l_con = ones(it_agridno,it_zgridno); fl_version = 3; % version 1 = numerical method, version 2 = vectorised, version 3 = taylor % series approximation for loop - has both vectorised and unvectorised % versions fl_vectorised = false; % for version 3- loop or vectorised
Version 1 - Numerical Method
if(fl_version == 1)
for i = 1:it_agridno*it_zgridno fl_a = ar_a_v(i); fl_z = ar_z_v(i); [ar_k_con(i),ar_l_con(i)] = conkl_numerical(fl_a,fl_z,fl_r,fl_w,fl_alpha,fl_theta,fl_kappa,fl_delta,fl_phi,fl_R); end ar_k_con = ar_k_con'; % transposing to get same order as input vector (it_agridnoxit_zgridno x 1) ar_l_con = ar_l_con'; % transposing to get same order as input vector (it_agridnoxit_zgridno x 1) mt_k_con = reshape(ar_k_con, [it_zgridno,it_agridno]); mt_l_con = reshape(ar_l_con, [it_zgridno,it_agridno]); mt_k_con = mt_k_con'; % getting to matrix of dimension it_agridnoxit_zgridno mt_l_con = mt_l_con'; % getting to matrix of dimension it_agridnoxit_zgridno
Version 2 - Vectorised solution
elseif (fl_version == 2)
ar_ks1 = linspace(0, 5*fl_ahi, it_k_n); % Grid of capital to search for roots of constraint equation (order = 1 X it_k_n) ar_ks = fliplr(ar_ks1); % flipping array to pick up the second root (non-zero root) f_lmax = @(z,k) (fl_w./((k.^fl_alpha).*fl_theta.*z)).^(1/(fl_theta - 1)); % max l for a given constrained k f_con_concave = @(a,z,k) fl_phi.*((k.^fl_alpha).*z.*(f_lmax(z,k)).^fl_theta - fl_w.*(f_lmax(z,k)))-(1+fl_r)*fl_kappa.*ones(numel(a),it_k_n)+(1+fl_r).*(a).*ones(1,it_k_n); % concave part of the constraint function f_con_straight = @(a,z,k) (1-fl_phi).*(1-fl_delta).*ones(numel(a),1).*k+fl_R.*ones(numel(a),1).*k; % straight line part of the constraint function f_con = @(a,z,k) f_con_concave(a,z,k) - f_con_straight(a,z,k); % constraint function f1 = f_con(ar_a_v, ar_z_v, ar_ks); % f1 evaulates the constraint for each combination of a,z and k. Order of f1 = ((it_agridnoxit_zgridno) X it_k_n) % for i=1:it_agridno*it_zgridno % f1(i,it_k_n)=-1000; % end f1(:,it_k_n) = -1000; % assigning a large absolute value to the constraint at k=0 so as to % remove the root k=0 [val, idx] = min(abs((f1)')); % for each combi of a,z, root of the constraint equation is the k for % which the value of the constraint function is closest to zero. % min function on a matrix minimizes over each column, min (NXM) is of % order (1XM). As f1 is of the order ((it_agridnoxit_zgridno) X it_k_n), % dimension of val and idx = (1 X (it_agridnoXit_zgridno)). Since we need to minimize f1 over % k for each combination of a and z, and dim f1=((it_agridnoxit_zgridno) X it_k_n), % dim f1' = (it_k_n x (it_agridnoxit_zgridno)), dim min(abs((f1)'))= 1 X (it_agridnoxit_zgridno), % dim val , idx = 1 X (it_agridnoxit_zgridno) [val2,idx2] = max(((f1)')); % store the max value of f1(k) for each combination of a,z ar_k_con = ar_ks(idx); % storing constrained k values, dim = 1 X (it_agridnoxit_zgridno) % Analysing cases where the only root of constraint equation is k=0 in % the range of k's we are checking % There are 2 subcases: % 1) k = 0 is the only root and max of f is obtained at k = 0 ( all other % f's are negative in the range of k's ) % 2) k = 0 is not the only root, but only root in the given range of k's % we are checking. The actual constrained k is very high in this case, % so assuming the optimal would surely be less than the constrained k for i=1:it_agridno*it_zgridno if (ar_k_con(i)==ar_ks1(2)) if (val2(i)<=0) ar_k_con(i)=0; % Case 1) else ar_k_con(i)=1000000; % Case 2) end end end % Limitation of this method is for case 2), if optimal k was greater than % constrained k, those cases you are not sure about (not sure if those % cases exist) ar_k_con = ar_k_con'; % transposing to get same order as input vector (it_agridnoxit_zgridno x 1) ar_l_con = (fl_w./(fl_theta.*ar_z_v.*ar_k_con.^(fl_alpha))).^(1/(fl_theta-1)); mt_k_con = reshape(ar_k_con, [it_zgridno,it_agridno]); mt_l_con = reshape(ar_l_con, [it_zgridno,it_agridno]); mt_k_con = mt_k_con'; % getting to matrix of dimension it_agridnoxit_zgridno mt_l_con = mt_l_con'; % getting to matrix of dimension it_agridnoxit_zgridno
Version 3 - Taylor Series Method - For loop
elseif (fl_version == 3) if(~fl_vectorised)
% Solving constraint k for each combination of a and z one by one. % The constraint function has a linear part and a curved part. % Starting at any point, the the curved part is approximated to a straight line with a taylor series expansion % The intersection of the first approximation and the linear part % is the first guess of k. At the first guess of k, approximate the % curve part again as a stright line, then find its intersection % with a straight line for the next guess of k. Continue doing that % until it_max_iter_taylor iterations (you converge to the correct k in less than those no. of iterations syms k w alph theta kappa r phi delta R for i = 1:it_agridno for j = 1:it_zgridno % Defining the functions using symbols only f_lmax = (w/((k^alph)*theta*ar_z(j)))^(1/(theta - 1)); % optimal l to constrained k f_con_concave = phi*((k^alph)*ar_z(j)*(f_lmax)^theta - w*(f_lmax))-(1+r)*kappa+(1+r)*(ar_a(i)); % Concave part of constraint function of k f_con_straight = (1-phi)*(1-delta)*k+R*k; % Straight line part of constraint function of k % Substituting parameters in the constraint function f_con_straight_sub = subs(f_con_straight,{w,alph,theta,kappa,r,phi,delta,R},{fl_w,fl_alpha fl_theta,fl_kappa,fl_r,fl_phi,fl_delta, fl_R}); f_con_concavej_k = subs(f_con_concave, {w,alph,theta,kappa,r,phi,delta,R}, {fl_w,fl_alpha fl_theta,fl_kappa,fl_r,fl_phi,fl_delta, fl_R}); m = 1; % no if iteration for guess of k kj = 1; % First guess of k % * a = constant term in taylor approximate of the concave part of constraint function % * b = coefficient of k in taylor approximate of the concave part of constraint function % * c = 0 (constant term of straight line part of constraint - staight line function chosen that way) % * d = coefficient of k of straight line part of constraint if (bl_state_test) ar_k_store = zeros(1, it_max_iter_taylor); % Store all values of guesses of k end if (fl_phi == 0) % assuming kappa = 0, id a = 0 and phi = 0, opti k = 0 mt_k_con(i,j) = (1+fl_r)*(ar_a(i)- fl_kappa); mt_l_con(i,j) = (fl_w/((mt_k_con(i,j)^fl_alpha)*fl_theta*ar_z(j)))^(1/(fl_theta - 1)); else
% bl_solution_exits = false; s=0; % s increases value when a<0, case where there is no intersection of the 2 straight lines while (m < it_max_iter_taylor) f_con_concavej = double(subs(f_con_concavej_k, {k}, {kj})); % substituting first guess of k % computing coefficients a and b of taylor series approximate f_con_concave_diff_k = diff(f_con_concave,k); f_con_concave_diff_kj = double(subs(f_con_concave_diff_k, {k,w,alph,theta,kappa,r,phi,delta,R}, {kj,fl_w,fl_alpha fl_theta,fl_kappa,fl_r,fl_phi,fl_delta, fl_R})); d = (1-fl_phi)*(1-fl_delta)+ fl_R; a = double(f_con_concavej-f_con_concave_diff_kj*kj); b = double(f_con_concave_diff_kj); if (b>d) % Case where slope of tangent to curve greater % than that of straight line), first guess needs to % a large no. k_jplus1=kj*100; elseif (a<0) %case where there is no intersection of the 2 straight lines k_jplus1 = kj; s=s+1; else k_jplus1 = (a/(d-b)); % intersection of taylor approximate and straight line part of the constraint end % Displaying coefficients of straight line and tangent to % curved part of the constraint, and each guess of k if (i == it_test_a_idx && j == it_test_z_idx && bl_state_test) st_test_iter_info_one = ['iter:', num2str(m), ', kj:', num2str(kj)]; st_test_iter_info_two = ['y-interp for lin approx of concave:', num2str(a)]; st_test_iter_info_thr = ['slope for lin approx of concave:', num2str(b)]; st_test_iter_info_fou = ['slope for origin linear line:', num2str(d)]; disp(st_test_iter_info_one); disp(st_test_iter_info_two); disp(st_test_iter_info_thr); disp(st_test_iter_info_fou); ar_k_store(m) = kj; % storing all k's which were guessed until convergence to root end % updating kj = k_jplus1; % next guess of k m = m+1; % updating iteration for next guess of k end %if(~bl_solution_exits) % display ('constraint equation has no positive solution for capital'); %return; %else mt_k_con(i,j) = kj; % updating constrained k for each a and z mt_l_con(i,j) = (fl_w/((kj^fl_alpha)*fl_theta*ar_z(j)))^(1/(fl_theta - 1)); if (s>0) mt_k_con(i,j)=0; mt_l_con(i,j)=0; end % updating optimal l to correponding constrained k for each a and z bl_state_test = true;
iter:1, kj:1 y-interp for lin approx of concave:11.3482 slope for lin approx of concave:0.81569 slope for origin linear line:0.57 iter:2, kj:100 y-interp for lin approx of concave:19.6933 slope for lin approx of concave:0.16711 slope for origin linear line:0.57 iter:3, kj:48.8799 y-interp for lin approx of concave:16.4067 slope for lin approx of concave:0.21381 slope for origin linear line:0.57 iter:4, kj:46.0613 y-interp for lin approx of concave:16.1971 slope for lin approx of concave:0.21822 slope for origin linear line:0.57 iter:5, kj:46.0439 y-interp for lin approx of concave:16.1958 slope for lin approx of concave:0.21825 slope for origin linear line:0.57 iter:6, kj:46.0439 y-interp for lin approx of concave:16.1958 slope for lin approx of concave:0.21825 slope for origin linear line:0.57
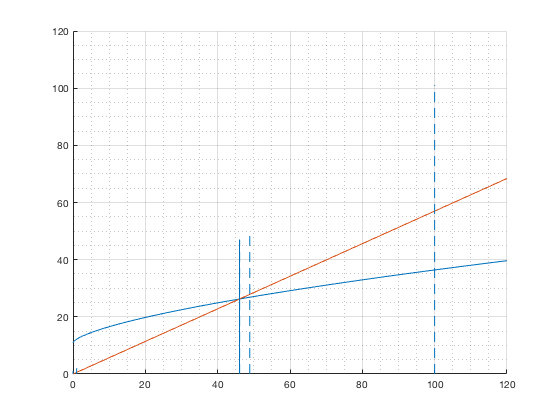
Graph Curve and line Intersection
if (i== it_test_a_idx && j == it_test_z_idx && bl_state_test) figure(1); hold on; %fl_k_max = min(0.001, kj + kj/10); fl_k_max = 120; fplot(f_con_concavej_k, [0, fl_k_max]); fplot(f_con_straight_sub, [0, fl_k_max]); for it_m = 1:1:it_max_iter_taylor fl_kj_cur = ar_k_store(it_m); line([real(fl_kj_cur) real(fl_kj_cur)],[0 fl_kj_cur+1], 'LineStyle', '--'); % -- lines are guesses of k end line([real(kj) real(kj)],[0 kj+1]); % final solution k grid on; grid minor; if(bl_saveimg) saveas(gcf, '/Users/sidhantkhanna/Documents/GitHub/BKS modified/code/Firms/figures/con_kl/taylor.png') end end
end end end mt_k_con1 = mt_k_con'; mt_l_con1 = mt_l_con'; ar_k_con = mt_k_con1(:); % matrix unlayered one column under another ar_l_con = mt_l_con1(:); % matrix unlayered one column under another
Version 3 - Taylor Series Method - Vectorised Version
elseif(fl_phi==0) ar_k_con =(1+fl_r).*(ar_a_v- fl_kappa.*ones(numel(ar_a_v),1)); ar_l_con =(fl_w./(fl_theta.*ar_z_v.*ar_k_con.^(fl_alpha))).^(1/(fl_theta-1)); ar_k_con(ar_k_con<0) = 0; ar_l_con(ar_l_con<0) = 0; mt_k_con=reshape(ar_k_con, [it_zgridno,it_agridno]); mt_l_con=reshape(ar_l_con, [it_zgridno,it_agridno]); mt_k_con=mt_k_con'; mt_l_con=mt_l_con'; else ar_kj = ones(it_agridno*it_zgridno, 1); % initial guess of k m = 1; s = zeros(it_agridno*it_zgridno, 1); s1 = zeros(it_agridno*it_zgridno, 1); while (m < it_max_iter_taylor) f_lmax = (fl_w./((ar_kj.^fl_alpha)*fl_theta.*ar_z_v)).^(1/(fl_theta - 1)); f_con_concave = fl_phi*((ar_kj.^fl_alpha).*ar_z_v.*(f_lmax).^fl_theta - fl_w.*(f_lmax))-(1+fl_r)*fl_kappa.*ones(it_agridno*it_zgridno,1)+(1+fl_r).*(ar_a_v); f_con_concave_diff = fl_phi.*(fl_alpha.*ar_kj.^(fl_alpha - 1).*ar_z_v.*((fl_w./(ar_kj.^fl_alpha.*fl_theta.*ar_z_v)).^(1/(fl_theta - 1))).^fl_theta - (fl_alpha.*ar_kj.^fl_alpha.*fl_w.*((fl_w./(ar_kj.^fl_alpha.*fl_theta.*ar_z_v)).^(1/(fl_theta - 1))).^(fl_theta - 1).*(fl_w./(ar_kj.^fl_alpha.*fl_theta.*ar_z_v)).^(1/(fl_theta - 1) - 1))./(ar_kj.^(fl_alpha + 1).*(fl_theta - 1)) + (fl_alpha.*fl_w^2.*(fl_w./(ar_kj.^fl_alpha.*fl_theta.*ar_z_v)).^(1/(fl_theta - 1) - 1))./(ar_kj.^(fl_alpha + 1).*fl_theta.*ar_z_v.*(fl_theta - 1))); d = ((1-fl_phi)*(1-fl_delta)+ fl_R).*ones(it_agridno*it_zgridno, 1); a = (f_con_concave-f_con_concave_diff.*ar_kj); b = f_con_concave_diff; % find k_{j+1} for everyone ar_k_jplus1 = (a./(d-b)); % ar_k_jplus1_dup = ar_k_jplus1; % replace if lin approximate for slope is greater than linear slope ar_k_jplus1((b>d)) = ar_kj(b>d)*100; % s1(b>d) = s1(b>d)+1; ar_k_jplus1((a<0) & (b<d)) = ar_kj(a<0 & b<d); s(a<0 & b<d) = s(a<0 & b<d)+1; ar_kj = ar_k_jplus1; m = m+1; end ar_k_con = ar_kj; ar_l_con = (fl_w./(fl_theta.*ar_z_v.*ar_k_con.^(fl_alpha))).^(1/(fl_theta-1)); ar_l_con1 = ar_l_con; ar_k_con(s>0) = 0; ar_l_con(s>0) = 0; % ar_k_con(s1>0) = ar_kj(s1>0); % ar_l_con(s1>0) = ar_l_con1(s1>0); mt_k_con=reshape(ar_k_con, [it_zgridno,it_agridno]); mt_l_con=reshape(ar_l_con, [it_zgridno,it_agridno]); mt_k_con=mt_k_con'; mt_l_con=mt_l_con'; end end
Print matrix for constrained k and l
if(bl_print) disp('mt_k_con'); disp(mt_k_con); disp('mt_l_con'); disp(mt_l_con); figure (2) surf(ar_z, ar_a, mt_k_con); title('K constraint given a and z'); xlabel('a'); ylabel('z'); zlabel('K constraint'); view(125,35); if(bl_saveimg) saveas(gcf, '/Users/sidhantkhanna/Documents/GitHub/BKS modified/code/Firms/figures/con_kl/Kconst_az.png') end figure (3) surf(ar_z, ar_a, mt_l_con); title('L constraint given a and z'); xlabel('a'); ylabel('z'); zlabel('L with K constrained'); view(125,35); if(bl_saveimg) saveas(gcf, '/Users/sidhantkhanna/Documents/GitHub/BKS modified/code/Firms/figures/con_kl/Lconst_az.png') end end if(bl_profile) profile off; profile viewer; st_file_name = '/Users/sidhantkhanna/Documents/GitHub/BKS modified/code/Profile/Firms/con_kl'; profsave(profile('info'), st_file_name); end
mt_k_con
0 0 0 6.0551 23.6750 89.4185
19.2580 22.3586 30.0059 46.0439 79.7481 149.5586
42.1321 47.1884 58.8345 80.8599 122.0637 199.4670
64.9941 71.6404 86.4906 113.2944 160.6981 245.0144
87.8497 95.8947 113.5405 144.4921 197.3334 287.9551
mt_l_con
0 0 0 2.8784 11.0640 37.6848
0.0405 1.2960 4.3926 10.8866 24.5341 52.8016
0.0677 2.1151 6.8308 15.7493 32.4335 63.7754
0.0900 2.7812 8.7943 19.6476 38.8422 72.9834
0.1096 3.3672 10.5123 23.0451 44.4416 81.1359